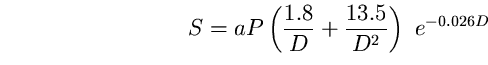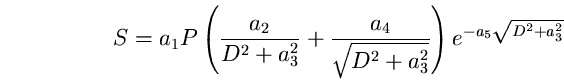


Next: Relazione Brillanza-Distanza per territori
Up: section
Previous: section
La brillanza del cielo causata da una città, ad una certa
distanza angolare z dallo zenith, varia con la distanza dalla
città.
Walker (1977) ha misurato la differenza Q tra la
brillanza del cielo a 45truept  dallo zenith, in direzione di una
città e nella direzione opposta, per diverse distanze dalla
città americana di Salinas (68600 abitanti). I valori di Q
ottenuti sono ben rappresentati in funzione della distanza D dalla
legge :
dallo zenith, in direzione di una
città e nella direzione opposta, per diverse distanze dalla
città americana di Salinas (68600 abitanti). I valori di Q
ottenuti sono ben rappresentati in funzione della distanza D dalla
legge :

(81)
Bertiau, de Graeve e Treanor (1973) hanno misurato nel 1971 la
brillanza del cielo allo zenith a diverse distanze dalle
città di Roma (2600000 abitanti), L'Aquila (61000 abitanti) e
Teramo (48000 abitanti). Essi sono riusciti ad ottenere un buon
accordo con le osservazioni per tutte e tre le città applicando
una legge di propagazione ottenuta da Treanor (1973) con un semplice modello
tenendo conto di una doppia diffusione in un modo simile a quello
illustrato nella sezione 2.4.2:
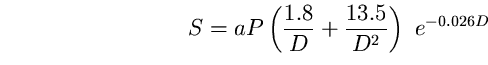
(82)
ove D è la distanza dalla sorgente di inquinamento luminosokm, P la
popolazione in unità di 105 , a è un coefficiente di
sviluppo economico, da essi introdotto, che per Roma vale 1, ed S
è in unità della brillanza naturale del cielo. Essi utilizzarono questa
legge per calcolare la brillanza del cielo prevista nel nostro Paese (Bertiau
et al.1973). I loro risultati sono illustrati nella figura 4.1 a pagina
![[*]](cross_ref_motif.gif) .
Walker (1977) provò ad applicare la legge di Bertiau, de Graeve e
Treanor (1973) alle sue osservazioni di Salinas ed ottenne un
generale accordo con i valori sperimentali fatta eccezione per
l'intervallo 24-35 km. Occorre tener presente però che la legge
si riferisce alla brillanza allo zenith mentre le osservazioni di
Walker si riferiscono alla differenza fra le brillanze a 45truept
.
Walker (1977) provò ad applicare la legge di Bertiau, de Graeve e
Treanor (1973) alle sue osservazioni di Salinas ed ottenne un
generale accordo con i valori sperimentali fatta eccezione per
l'intervallo 24-35 km. Occorre tener presente però che la legge
si riferisce alla brillanza allo zenith mentre le osservazioni di
Walker si riferiscono alla differenza fra le brillanze a 45truept  verso la città e dalla parte opposta. Quindi non ci si può
aspettare nulla di più di un accordo approssimativo.
verso la città e dalla parte opposta. Quindi non ci si può
aspettare nulla di più di un accordo approssimativo.
Un espressione simile a quella di Bertiau, de Graeve e Treanor
(1973) è stata
proposta da) Berry (1976):
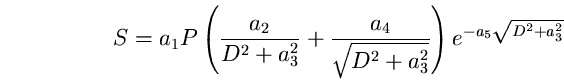
(83)
ove a1 , a2 , a3 , a4 e a5 sono costanti, P
è la popolazione, D la distanza e la brillanza S va misurata in
S10 (si veda il capitolo sulle unità di misura).
Modelli più complessi (Garstang 1986) mostrano che la brillanza
del cielo allo zenith decresce con la distanza in modo non
lineare. Se si scrive

(84)
si trova che il coefficiente 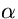 diventa più negativo al
crescere della
distanza e, per città molto popolate capaci di inviare luce anche
molto
lontano, può arrivare anche ad
diventa più negativo al
crescere della
distanza e, per città molto popolate capaci di inviare luce anche
molto
lontano, può arrivare anche ad 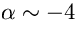 . L'esponente
. L'esponente
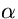 diventa più negativo
anche al crescere della percentuale di aerosoli rispetto alle
molecole, cioè
al diminuire della limpidezza dell'aria.
diventa più negativo
anche al crescere della percentuale di aerosoli rispetto alle
molecole, cioè
al diminuire della limpidezza dell'aria.
Garstang (1989) ha mostrato come l'effetto della curvatura della
superficie
terrestre non è trascurabile per distanze oltre i 50 km e fa si
che la
brillanza dovuta alle grandi città molto distanti decresca più
di quanto
accadrebbe se la terra fosse piatta. Alla distanza di 50 km la
differenza nella
brillanza vicino allo zenith tra i risultati di modelli che
tengano conto o
meno della curvatura terrestre è del 2% circa.
L'effetto della foschia e, in generale, l'effetto di un aumento
della quantità di
aerosoli consiste nell'aumentare la brillanza del cielo allo
zenith nelle vicinanze delle sorgenti di inquinamento luminoso
effetto dell'aumento della diffusione. Tuttavia la brillanza
decresce in luoghi
situati sufficientemente lontano dalle sorgenti per effetto
dell'aumento dell'estinzione .



Next: Relazione Brillanza-Distanza per territori
Up: section
Previous: section
Pierantonio Cinzano
3/12/1998

![]() dallo zenith, in direzione di una
città e nella direzione opposta, per diverse distanze dalla
città americana di Salinas (68600 abitanti). I valori di Q
ottenuti sono ben rappresentati in funzione della distanza D dalla
legge :
dallo zenith, in direzione di una
città e nella direzione opposta, per diverse distanze dalla
città americana di Salinas (68600 abitanti). I valori di Q
ottenuti sono ben rappresentati in funzione della distanza D dalla
legge :